目录:
一、汉诺塔
二、课时24课后习题及答案
*************
一、汉诺塔
*************
汉诺塔:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。

对于游戏的玩法,我们可以简单分解为三个步骤
(1)将前63个盘子从X移动到Y上。
(2)将最底下的第64个盘子从X移动到Z上。
(3)将Y上的63个盘子移动到Z上。
仔细想下,在游戏中,我们发现每次都只能移动一个圆盘,所以在移动的过程中显然要借助另外一根针才可以实施。也就是说,步骤(1)将1~63个盘子需要借助Z移到Y上,步骤(3)将Y针上的63个盘子需要借助X移到Z针上。
所以把新思路聚集为以下两个问题:
问题一:将X上的63个盘子借助Z移到Y上;
问题二:将Y上的63个盘子借助X移到Z上。
可以拆分为3个步骤来实现:
问题一(“将X上的63个盘子借助Z移到Y上”)拆解为:
(1)将前62个盘子从X移动到Z上。
(2)将最底下的第63个盘子移动到Y上。
(3)将Z上的62个盘子移动到Y上。
问题二(“将Y上的63个盘子借助X移到Z上”)拆解为:
(1)将前62个盘子从Y移动到X上。
(2)将最底下的第63个盘子移动到Z上。
(3)将X上的62个盘子移动到Y上。
说到这里,你发现了什么?没错,汉诺塔的拆解过程刚好满足递归算法的定义,因此,对于如此难题,使用递归来解决,问题就变得相当简单。参考代码:
def hanoi(n, x, y, z):
if n == 1:
print(x, ' --> ', z)
else:
hanoi(n-1, x, z, y) # 将前n-1个盘子从x移动到y上
print(x, ' --> ', z) # 将最底下的最后一个盘子从x移动到z上
hanoi(n-1, y, x, z) # 将y上的n-1个盘子移动到z上
n = int(input('请输入汉诺塔的层数:'))
hanoi(n, 'X', 'Y', 'Z')
看!这就是递归的魔力。
*******************************
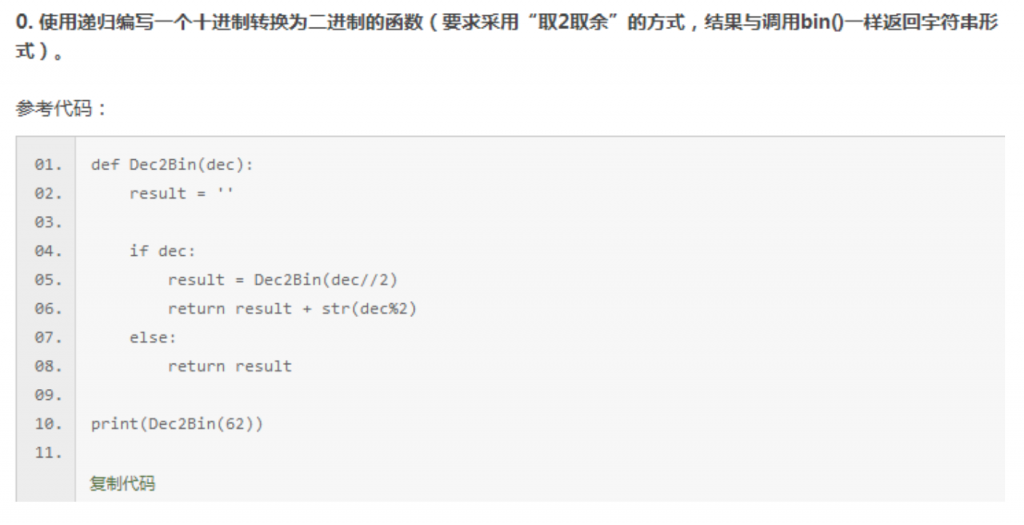
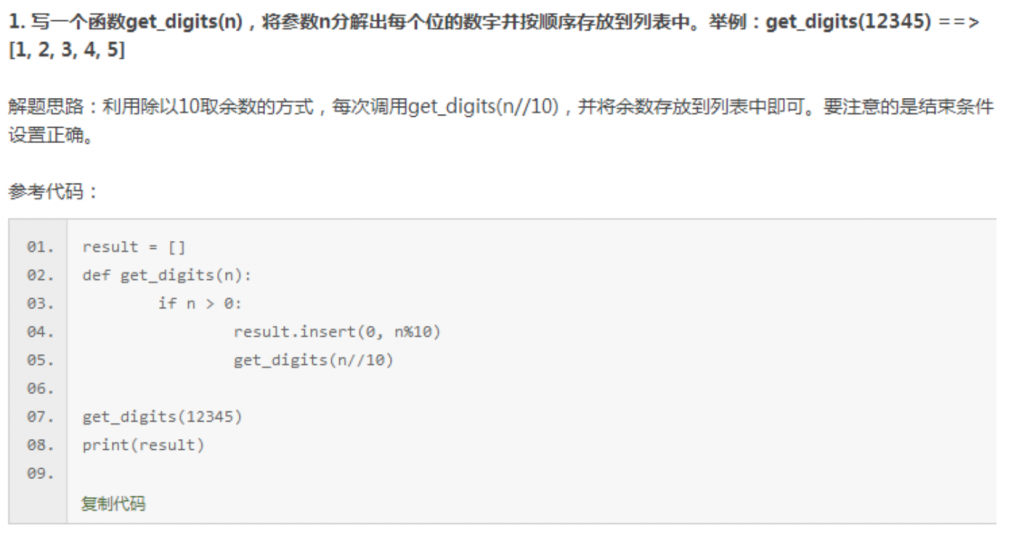
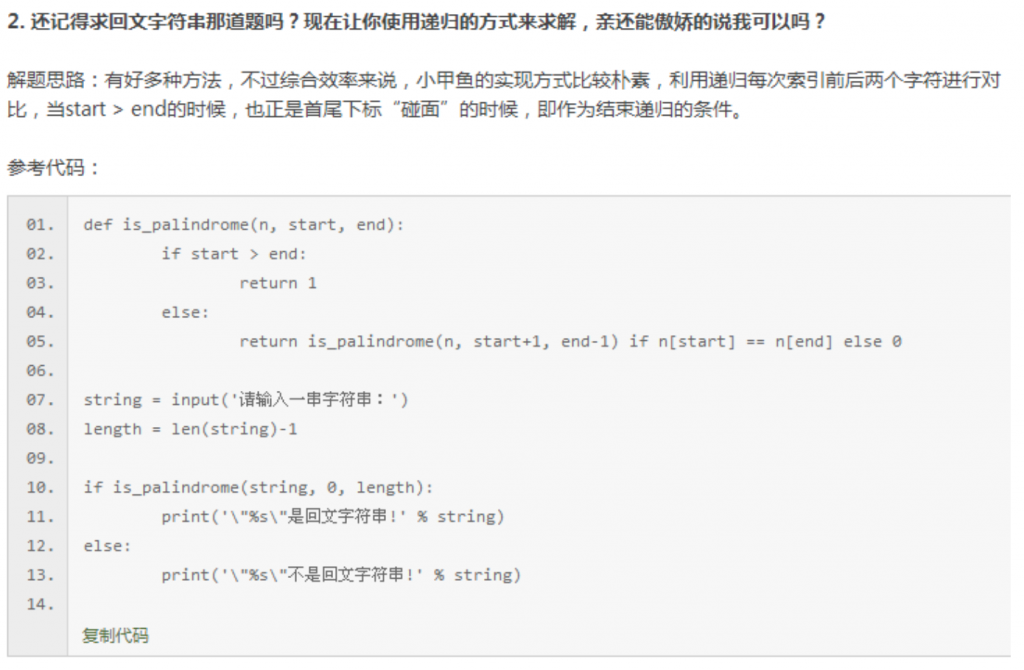
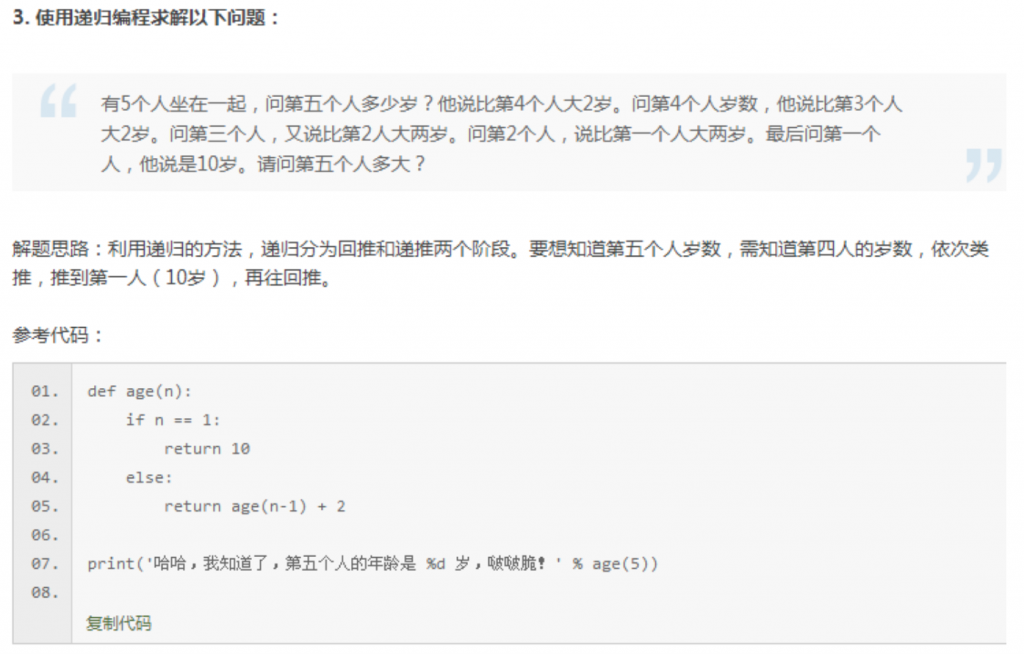
二、课时24课后习题及答案
*******************************