目录：

　　斐波那契数列

****************

斐波那契数列

****************

这节就用递归来实现斐波那契数列。首先，我们要知道斐波那契的发明者，是意大利数学家昂纳多.斐波那契。

我们都知道兔子的繁殖能力惊人，如图所示：

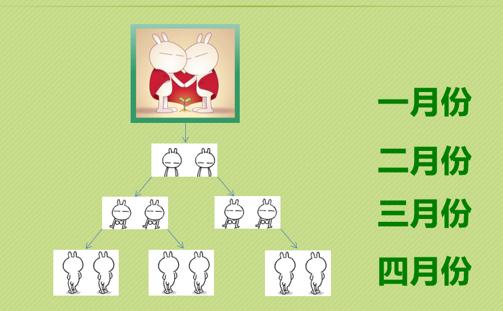
数据统计表如下图所示：

迭代实现：

def fab(n):
    n1 = 1
    n2 = 1
    n3 = 1

    if n < 1:
        print('输入有误！')
        return -1

    while (n-2) > 0:
        n3 = n2 + n1
        n1 = n2
        n2 = n3
        n -= 1
    
    return n3

result = fab(45)
if result != -1:
    print('总共有%d对小兔崽子诞生！' % result)

接下来看看递归的实现原理,如图所示：

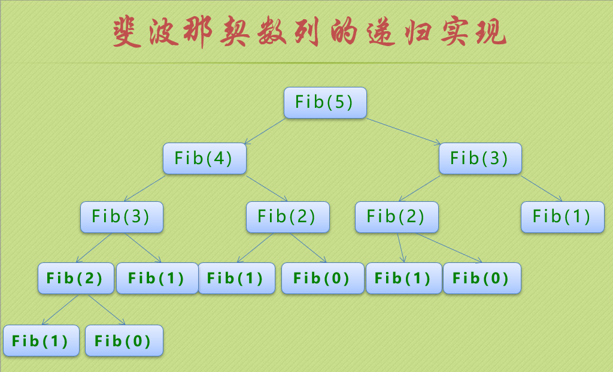
递归实现：

def fab(n):
    if n < 1:
        print('输入有误！')
        return -1

    if n == 1 or n == 2:
        return 1
    else:
        return fab(n-1) + fab(n-2)

result = fab(35)
if result != -1:
    print('总共有%d对小兔崽子诞生！' % result)

可见逻辑非常简单，直接把想的东西写成代码就是递归算法了。不过在之前我们总说递归如果使用不当，效率会很低，但是有多低呢？我们试图把20个月修改为35个月，然后运行程序….

发现了吧，用迭代代码来实现基本是毫秒级的，而用递归来实现就考验你的CPU能力啦（N秒~N分钟不等）。这就是小甲鱼不支持大家所有东西都用递归求解的原因，本来好好的一个代码，给你用了递归，效率反而拉下了一大截。

为了体现递归正确使用的优势，下一节，我们谈谈利用递归解决汉诺塔难题。

这里可以在线玩个游戏，大家不妨边玩边思考代码怎么实现的：http://www.kaixin001.com/flashgame/game/10406.html